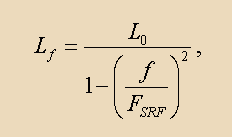 (2.1)
(2.1)
© И.Мамонтов, 2020, 2021.
(* часть информации взята из [1])
Весь двадцатый век прошел под знаком «собственной емкости».
Еще давно было замечено, что прямолинейный или свернутый в спираль проводник резонирует на определенных частотах. Первое систематическое учение о собственном резонансе было опубликовано немецким физиком Paul Drude в 1902 г. Он исследовал множество катушек с эбонитовым сердечником и без, которые покрывали широкий диапазон размеров. [Zur construction von Teslatransformatoren. Schwingungsdauer und Selbstinduction von Drahtspulen (On the construction of Tesla transformers: Period of oscillation and self-inductance of the coil). P Drude, 1902, Ann. Phys. 314 (10) p.293-339, 314 (11) p590-610. Английский перевод доступен по адресу: https://www.researchgate.net/publication/301624796, дата обращения 27.03.2010.].
Техника развивалась, необходимость в точных расчетах росла, и почти сразу появилась идея замещать катушку колебательным контуром, состоящим из параллельно соединенных индуктивности и емкости. Эта емкость получила название «собственной емкости» («self capacitance») и широко вошла в обиход. Такая модель более-менее оправдывала себя и была принята в широких кругах, а теоретиков заинтересовал вопрос, что же из себя представляет эта емкость, и можно ли ее рассчитать? Казалось очевидным, что она заключена в промежутке между витками.
В 1934 г. A.J.Palermo предложил формулу, основанную на наличии распределенной емкости между витками [Distributed Capacity of Single-Layer Coils, A J Palermo. Proc. IRE. Vol 22, No. 7, July 1934. p.897-905. 73]. Для подтверждения своей теории он привел данные измерений 19-ти катушек, 12 из которых получил сам, а остальные ему предоставил F.W.Grover из Национального Бюро Стандартов. Как отмечает D.W.Knight в своей работе [1], это подтверждение получилось очень натянутым, в частности, Palermo даже сфальсифицировал значения, которые дает его формула, чтобы они лучше соответствовали результатам измерений. Впоследствии было проведено множество измерений, опровергающих формулу Palermo, но, тем не менее, теория распределенной межвитковой емкости получила широкое распространение и вошла в инженерный обиход, а на основе формулы Palermo были построены таблицы и номограммы.
В 1935 г. Willis Jackson сообщил об измерениях индуктивностей и резонансных частот «свободно висящих» катушек с последующим вычислением их собственных емкостей по формуле Томпсона [The self-capacitance of single-layer coils. W Jackson. Phil. Mag. Ser. 7, Vol. 19, 128. Apr. 1935. p.823-835.]. Эти данные долгое время являлись источником трудностей при их интерпретации для случаев, где катушка включена в какую-либо цепь.
Неудовлетворенность формулой Palermo привела к тому, что в 1947 г. появился классический труд R.G.Medhurst «Сопротивление на высоких частотах и собственная емкость однослойных соленоидов» [H. F. Resistance and Self-Capacitance of Single-Layer Solenoids. R G Medhurst (GEC Research Labs.). Wireless Engineer, Feb. 1947 p.35-43, Mar. 1947 p.80-92. Corresp. June 1947 p.185, Sept. 1947 p.281.], где на основе измерений множества различных катушек предложена эмпирическая формула, хорошо предсказывающая результат. Измерения показали, что «собственная емкость» катушек зависит только от ее диаметра и пропорций («форм-фактора») и никоим образом не связана ни с шагом намотки, ни с диаметром провода, что в корне противоречит формуле Palermo. Казалось бы, теории, основанной на межвитковой емкости, должен быть положен конец.
Тем не менее в 1999 г. группой исследователей, состоящей из G.Grandi, M.K.Kazimierczuk, A.Massarini и U.Reggiani, производится попытка пересмотра этой теории [Stray Capacitances of Single-Layer Solenoid Air-Core Inductors. G. Grandi, M K Kazimierczuk, A Massarini, U Reggiani. IEEE Transactions on Industry Applications, Vol 35, No. 5, Sept/Oct 1999, p1162-1168.].
Их подход рассматривет катушку как набор изолированных колец из круглого проводника. Суммарная емкость такого «пакета» в N-1 раз (по числу зазоров) меньше емкости между двумя соседними кольцами. Кольца они «разворачивают» в систему из параллельных проводников и применяют к ней известную формулу Русселя (Russell) для емкости между двумя параллельными цилиндрами. Все изыскания были связаны с измерением емкости между кольцами и показали, что форма проводников (дуга вместо прямого отрезка) мало влияет на взаимную емкость, а влиянием соседних колец на исследуемый зазор можно пренебречь. Для проверки формулы использовалась только одна катушка, собственная емкость которой также рассчитывалась на основе измерения индуктивности и резонансной частоты, и которая «подтверждала» их теорию. Тот факт, что исследователи ограничились только одной катушкой, наводит на определенные размышления.
Немногим ранее, в 1988 г., F.S.Chute и F.E.Vermeulen использовали другую модель, основанную на представлении, что пространство между крайними витками заполнено неким «метаматериалом» [On the self-capacitance of solenoidal coils. F S Chute and F E Vermeulen. Canadian Elec. Eng. J.,Vol 7(2), 1982, p.31-37]. Их формула, по сравнению с формулой Palermo, дает более точные предсказания, т.к. исключает шаг намотки, однако зависимость первого порядка от диаметра провода остается.
В 2006 г. Дэвид Найт (D.W.Knight) начинает анализировать все известные подходы и экспериментальные данные, что выливается в более точную формулу «DAE» («Doubly-Asymptotic, Empirically corrected» – «двойная асимптотическая с эмпирической коррекцией»). Эта формула справедлива для широкого диапазона форм-факторов и учитывает влияние материала каркаса [The self-resonance and self-capacitance of solenoid coils, D W Knight, 2006 - 2013. – URL: http://www.g3ynh.info/zdocs/magnetics/appendix/self_res/self-res.pdf, дата обращения 27.03.2015]. Знаменательным в этой работе является то, что отрицается межвитковая емкость как первопричина образования «собственной емкости», а сама катушка рассматривается как однопроводная линия передачи, свернутая в спираль, у которой помимо осевой (продольной) компоненты электрического поля присутствует гораздо более сильная круговая (поперечная) компонента, обусловленная наличием переменного магнитного поля. Поскольку эта компонента доминирует, то именно она и отвечает за «собственную емкость». Продольная же компонента (которую можно было бы увязать с межвитковой емкостью) в заметном количестве имеется только у очень коротких катушек.
Следует заметить, что эта работа находится в стадии развития, а в 2016 г. появилась ее новая редакция (заменила предыдущую и находится по тому же адресу, дата обращения 03.11.2020), где автор отдает предпочтение волновому подходу, рассматривая катушку как резонирующую однопроводную линию передачи и продвигая мысль, что «собственная емкость» – величина кажущаяся. Рассчитать ее можно, зная резонансную частоту линии, которая, в свою очередь, зависит от способа включения (заземлены ли концы), общей длины проводника и локальной скорости распространения волны. Последняя зависит от форм-фактора и может даже превышать скорость света (что, однако, не противоречит законам природы, поскольку это всего лишь фазовая скорость, а не скорость распространения энергии). Подключение дополнительных цепей к концам такой катушки-линии сильно изменяет ее поведение, но количественных оценок автор не деает.
Еще дальше и радикальнее идет Алан Пэйн (Alan Payne) в статье «Self-resonance in coils and the self-capacitance myth» от 2014 г. [URL: http://g3rbj.co.uk/, дата обращения 19.03.2020], где напрочь отвергается существование собственной емкости (полагается равной нулю), а вместо этого индуктивность считается увеличивающейся по мере приближения рабочей частоты f к частоте собственного резонанса FSRF :
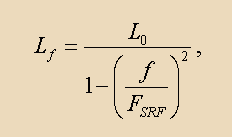 (2.1)
(2.1)
(Lo – значение индуктивности, измеренное на низкой частоте). Величина FSRF (в соответствии с волновой теорией) определяется длиной проводника, фазовой скоростью распространения волны и концевым эффектом (коррекцией длины катушки на величину, равную 0,45 от ее диаметра для свободной катушки, и 0,225 для катушки с заземленным концом). Для двух способов включения приводятся две формулы расчета FSRF , однако для проверки также используется только одна катушка. Делая упор на расчет FSRF , никаких рекомендаций относительно расчета влияния подсоединенного конденсатора на частоту резонанса автор не дает. Предполагается, видимо, что будет использоваться традиционная формула для резонансной частоты контура с оговоркой, что в качестве индуктивности следует использовать величину, определяемую формулой (2.1). Между тем, эта формула была выведена не им, а взята из работы Welsby V.G. «Теория и конструирование катушек индуктивности» [Welsby V.G.: The Theory and Design of Inductance Coils, Second edition, 1960, Macdonald, London], где волновые процессы не рассматриваются и используется традиционный подход с участием «собственной емкости» и жонглирование эквивалентностями. Это напоминает ситуацию, когда и провожающий прав, говоря что поезд начал двигаться, и пассажир, который утверждает, что относительно него «поехал» перрон. Таким образом, подход Алана Пэйна оказывается не лучше и не хуже традиционного – просто это две стороны одной медали. Тем не менее, представляет интерес принять сторону Алана Пэйна – хотя бы потому, что волновая теория дает как раз индуктивный характер входного сопротивления линии, замкнутой на конце, и его рост по мере приближения к первому резонансу.
Далее будет показано, как на основе зависимостей, взятых из теории длинных линий, вывести формулу, дающую более точный результат.
(полный текст находится здесь: <ссылка >)
[1] David W Knight. The self-resonance and self-capacitance of solenoid coils. – URL: http://g3ynh.info/zdocs/magnetics/ (19.03.2020).
[2] Payne A N. Self-Resonance in Coils. – URL: http://g3rbj.co.uk/ (19.03.2020).
[3] Асеев П.Б. Колебательные цепи. – М.: Государственное издательство литературы по вопросам связи и радио, 1955
http://antiradio.narod.ru/raznoe/about-self-C-F/
Дата создания документа: 19.03.2020. Последнее обновление: 24.01.2022.